中学生 数学 図形の性質と証明
中学2年生の数学では、図形の性質と証明という単元を学習します。
合同の証明や図形の定義、性質など、暗記すべき項目が非常に多い単元となります。
以下、中学2年生の単元で合同に関連するものをまとめました。
三角形の合同条件
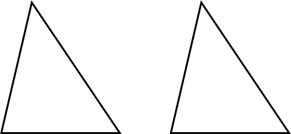
三角形の合同条件は次の「三角形の合同条件を見る」をクリックすると確認できます。(暗記に活用可)
三角形の合同条件を見る
① 3組の辺がそれぞれ等しい
② 2組の辺とその間の角がそれぞれ等しい
③ 1組の辺とその両端の角がそれぞれ等しい
直角三角形の合同条件
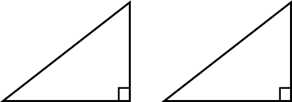
直角三角形の合同条件は次の「直角三角形の合同条件を見る」をクリックすると確認できます。(暗記に活用可)
直角三角形の合同条件を見る
① 斜辺と1つの鋭角がそれぞれ等しい
② 斜辺と他の1辺がそれぞれ等しい
二等辺三角形
二等辺三角形における「定義」「性質」と「二等辺三角形になるための条件」は次の通りです。
二等辺三角形の定義を見る
定義:2辺の長さが等しい
二等辺三角形の性質を見る
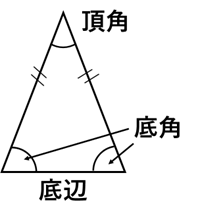
性質:2つの低角は等しい。頂角の二等分線は底辺を垂直に二等分する。
二等辺三角形になるための条件を見る
二等辺三角形になるための条件:2つの底角が等しい
正三角形
正三角形における「定義」「性質」と「正三角形になるための条件」は次の通りです。
正三角形の定義を見る
定義:3辺の長さが等しい
正三角形の性質を見る
性質:3つの角は全て等しい(60°)。中線はすべて1点(重心)で交わり、頂点の方向から2:1に分割される
正三角形になるための条件を見る
正三角形になるための条件:3つの角が等しい
平行四辺形
平行四辺形における「定義」「性質」と「平行四辺形になるための条件」は次の通りです。
平行四辺形の定義を見る
定義:2組の対辺がそれぞれ平行な四角形を平行四辺形という
平行四辺形の性質を見る
性質
① 2組の対辺はそれぞれ等しい。
② 2組の対角はそれぞれ等しい。
③ 対角線はそれぞれの中点で交わる。
平行四辺形になるための条件を見る
① 2組の対辺がそれぞれ平行である。
② 2組の対辺がそれぞれ等しい。
③ 2組の対角がそれぞれ等しい。
④ 対角線がそれぞれの中点で交わる。
⑤ 1組の対辺が平行でその長さが等しい。
長方形
長方形における「定義」「性質」と「長方形になるための条件」は次の通りです。
長方形の定義を見る
定義:4つの角が等しい四角形を長方形と言う。
長方形の性質を見る
性質:長方形の対角線の長さは等しい
長方形になるための条件を見る
① 対角線の長さが等しい平行四辺形は長方形である。
② となり合う2つの角が等しい平行四辺形は長方形である。
ひし形
ひし形における「定義」「性質」と「ひし形になるための条件」は次の通りです。
ひし形の定義を見る
定義:4つの辺が等しい四角形をひし形という。
ひし形の性質を見る
性質:ひし形の対角線は垂直に交わる
ひし形になるための条件を見る
① 対角線が垂直に交わる平行四辺形はひし形である。
② となり合う2つの辺の長さが等しい平行四辺形はひし形である。
正方形
正方形における「定義」「性質」と「正方形になるための条件」は次の通りです。
正方形の定義を見る
定義:4つの角が等しく、4つの辺が等しい四角形を正方形という。
正方形の性質を見る
性質:正方形の対角線は、長さが等しく、垂直に交わる。
正方形になるための条件を見る
正方形になるための条件:長方形になる条件とひし形の条件を両方持つ平行四辺形は正方形である。
定義や合同条件の暗記方法
「性質」や「合同条件」は、図形をもとに、イメージで覚えると良いでしょう。
合同条件や性質は、証明の問題の際に出題されますので、証明の問題を解きつつ、どこがどのような状態になっているのかを正確に捉えていくことで、正答率が上がります。
数学はあらゆる問題でイメージが重要となってきます。文章の羅列として暗記するのではなく、頭の中に図形を描いて考察すると良いでしょう。図形のイメージが湧かない場合は、図形と触れる回数が不足しています。たくさん問題を解き、一つ一つの形を捉えられるように練習しましょう。
一方で、定義が聞かれる問題は、高校入試においてごく稀に出題されます。定義は図形として覚えようとしても、性質や合同条件と混ざってしまいかねないため、余力があれば、定義を文章で暗記しておくと良いでしょう。
最後までご覧くださりありがとうございました。
