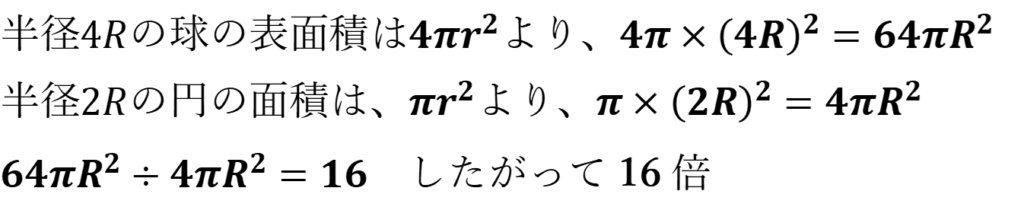MENU

中学2年生　数学　式の計算

目次

中学2年生　数学　式の計算

中学2年生の数学で学習する「式の計算」の単元の基本内容をまとめました。

ここに掲載されている例題をすべて自力で解けるならば、この単元の基礎が十分に備わっていると思います。

解答を見るを開くと、解説が表示されます。

式の計算　語句の確認

単項式　…　たし算や引き算の無いもの
多項式　…　たし算や引き算のあるもの
項　…　±の前で区切ったときの値
次数　…　1つの項でかけられた文字の個数の最大値
係数　…　文字にかけられている数字
同類項　…　文字と次数が同じ項

さらに詳しく

単項式　…　たし算や引き算の無いもの
多項式　…　たし算や引き算のあるもの
項　…　±の前で区切ったときの値
次数　…　1つの項でかけられた文字の個数の最大値
係数　…　文字にかけられている数字
同類項　…　文字と次数が同じ項

式の計算　基本例題

基本例題1

次の式の項と係数を答えなさい。

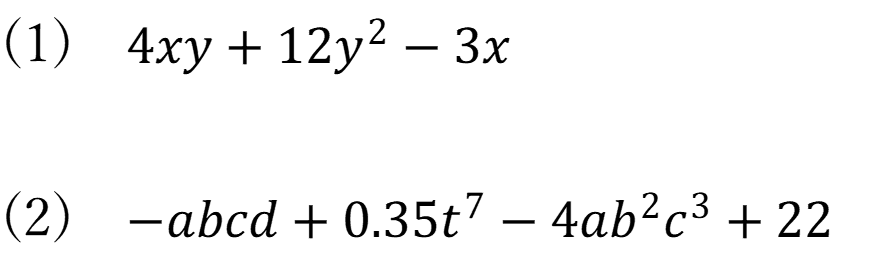
(1)　4xy+12y^2-3x

(2)　-abcd+0.35t^7-4ab^2c^3+22

解答を見る

(1)　4xy+12y^2-3x
項：4xy、12y^2、-3x
係数：xyの係数4、y^2の係数12、xの係数-3

(2)　-abcd+0.35t^7-4ab^2 c^3+22
項：-abcd、0.35t^7、-4ab^2 c^3、22
係数：abcdの係数-1、t^7の係数0.35、ab^2 c^3の係数-4

基本例題2

次の式の次数を答えなさい。

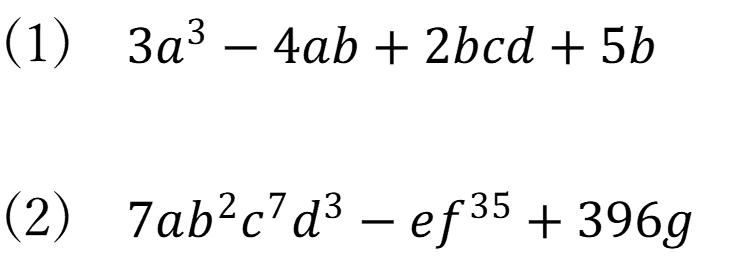
(1)　3a^3-4ab+2bcd+5b

(2)　7ab^2 c^7 d^3-ef^35+396g

解答を見る

(1)　3a^3-4ab+2bcd+5b
3a^3の項は3次、-4abの項は2次
2bcdの項は3次、5bの項は1次
最も次数の大きい項の次数が式の次数であるため、3次

(2)　7ab^2 c^7 d^3-ef^35+396g
7ab^2 c^7 d^3の項はa^1 b^2 c^7 d^3より、1+2+7+3=13次
-ef^35の項はe^1 f^35より、1+35=36次
396gの項はg^1より1次
最も次数の大きい項の次数が式の次数であるため、36次

基本例題3

次の式を計算しなさい。

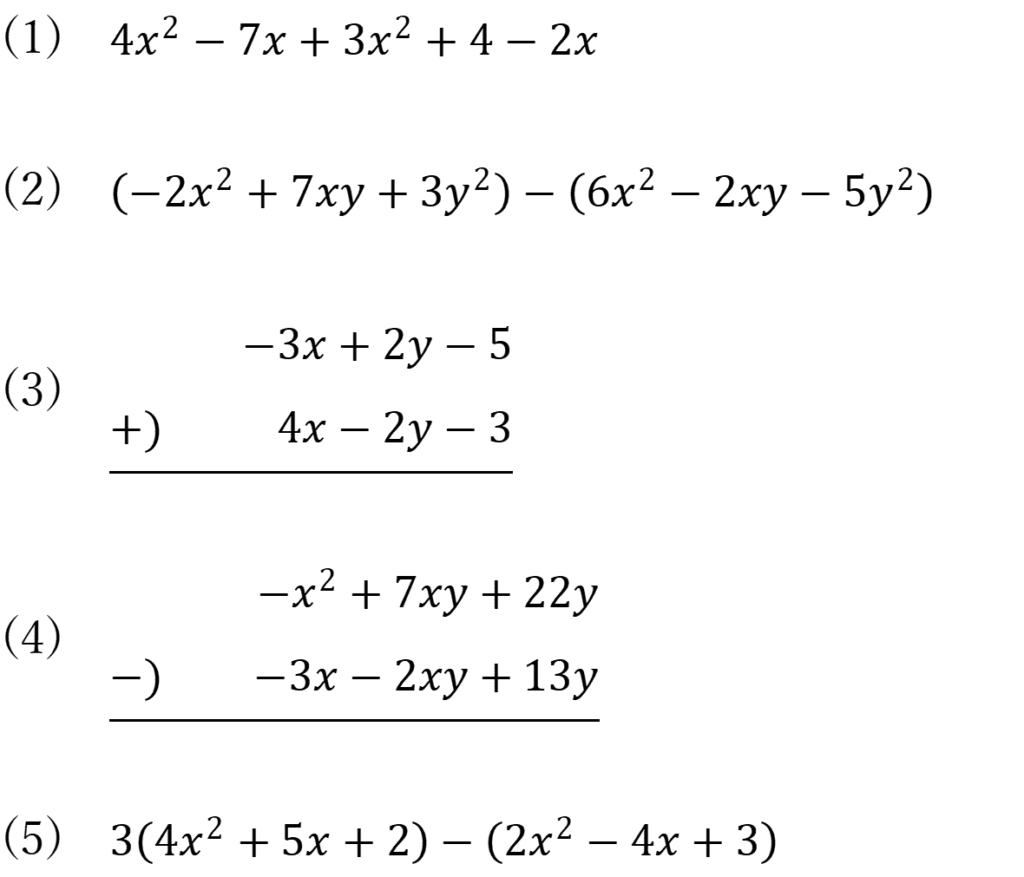
(1)　4x^2-7x+3x^2+4-2x

(2)　(-2x^2+7xy+3y^2 )-(6x^2-2xy-5y^2 )

(3)　■(■(　　　&-3x+2y-5)@▁(■(+)　　&　4x-2y-3)))

(4)　■(■(　　　&-x^2+7xy+22y)@▁(■(-)　　&-3x-2xy+13y)))

(5)　3(4x^2+5x+2)-(2x^2-4x+3)

解答を見る

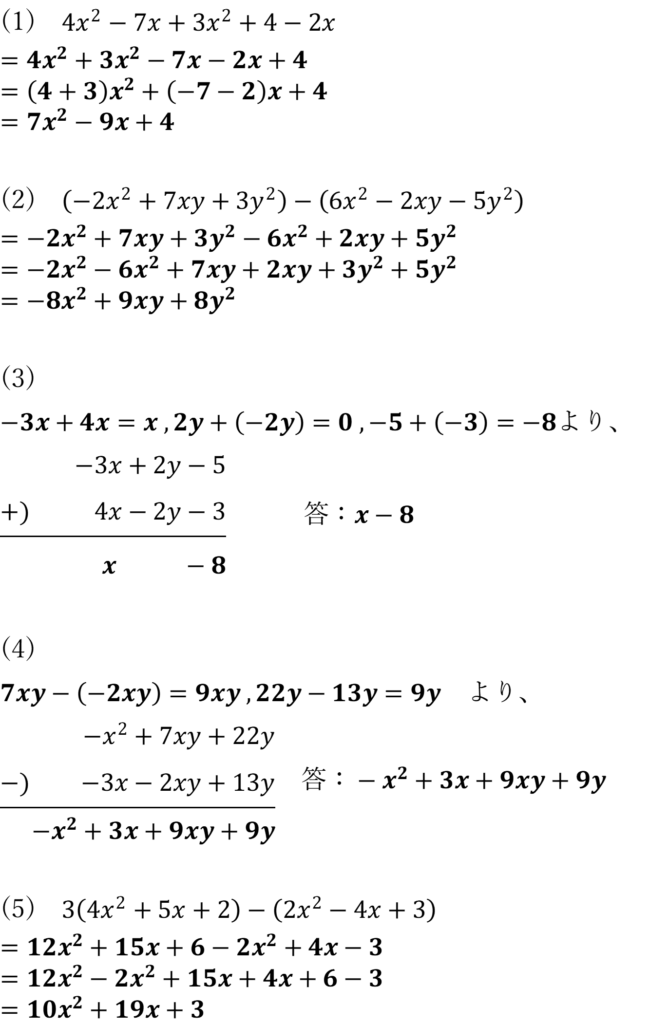
(1)　4x^2-7x+3x^2+4-2x
=4x^2+3x^2-7x-2x+4
=(4+3) x^2+(-7-2)x+4
=7x^2-9x+4

(2)　(-2x^2+7xy+3y^2 )-(6x^2-2xy-5y^2 )
=-2x^2+7xy+3y^2-6x^2+2xy+5y^2
=-2x^2-6x^2+7xy+2xy+3y^2+5y^2
=-8x^2+9xy+8y^2

(3)　
-3x+4x=x ,2y+(-2y)=0 ,-5+(-3)=-8より、
■(▁(■(■(　　　&-3x+2y-5)@■(+)　　&　4x-2y-3)))@x　　　　　-8)　　　答：x-8

(4)　
7xy-(-2xy)=9xy ,22y-13y=9y　より、
■(▁(■(■(　　　&-x^2+7xy+22y)@■(-)　　&-3x-2xy+13y)))@-x^2+3x+9xy+9y)　答：-x^2+3x+9xy+9y

(5)　3(4x^2+5x+2)-(2x^2-4x+3)
=12x^2+15x+6-2x^2+4x-3
=12x^2-2x^2+15x+4x+6-3
=10x^2+19x+3

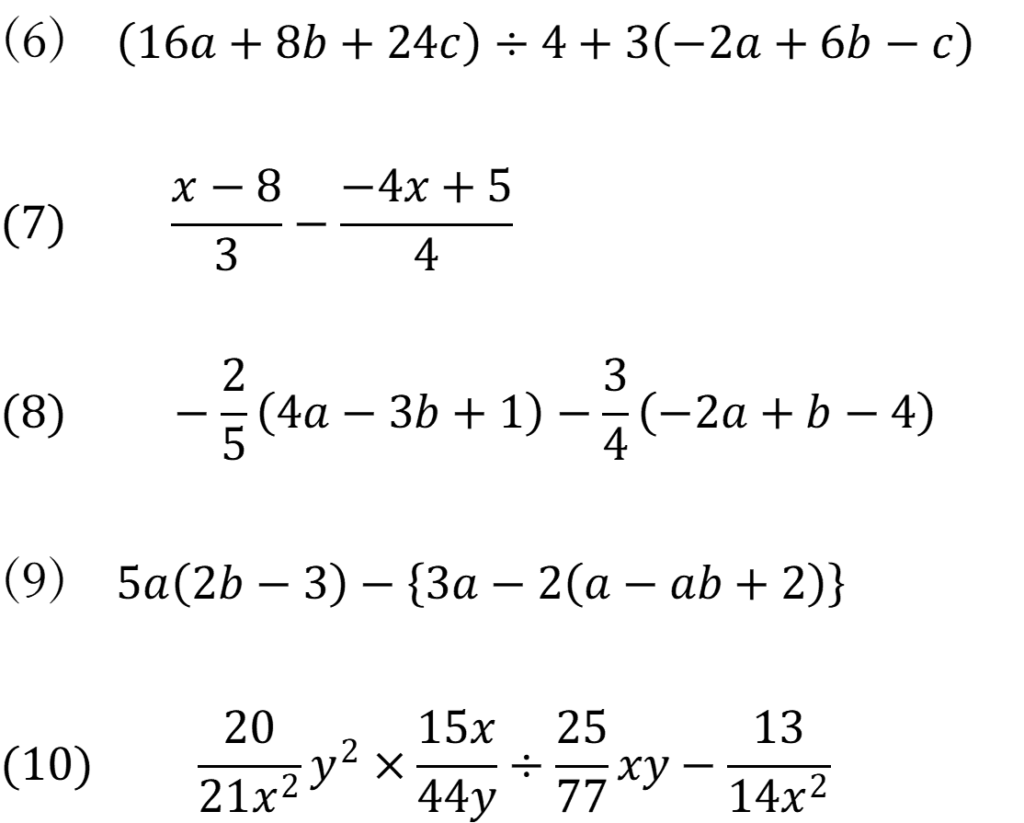
(6)　(16a+8b+24c)÷4+3(-2a+6b-c)

(7)　　(x-8)/3-(-4x+5)/4

(8)　　-2/5 (4a-3b+1)-3/4 (-2a+b-4)

(9)　5a(2b-3)-{3a-2(a-ab+2)}

(10)　　20/(21x^2 ) y^2×15x/44y÷25/77 xy-13/(14x^2 )

解答を見る

(6)　(16a+8b+24c)÷4+3(-2a+6b-c)
=4a+2b+6c-6a+18b-3c
=4a-6a+2b+18b+6c-3c
=-2a+20b+3c

(7)　　(x-8)/3-(-4x+5)/4
=4(x-8)/12-3(-4x+5)/12=(4x-32)/12-(-12x+15)/12
=(4x-32+12x-15)/12=(26x-47)/12

(8)　　-2/5 (4a-3b+1)-3/4 (-2a+b-4)
=-2/5×4a-2/5×(-3b)-2/5-3/4×(-2a)-3/4 b-3/4×(-4)
=-8/5 a+6/5 b-2/5+3/2 a-3/4 b+3
=-8/5 a+3/2 a+6/5 b-3/4 b-2/5+3
=-16/10 a+15/10 a+24/20 b-15/20 b-2/5+15/5
=-1/10 a+9/20 b+13/5

(9)　5a(2b-3)-{3a-2(a-ab+2)}
=10ab-15a-(3a-2a+2ab-4)
=10ab-15a-(a+2ab-4)
=10ab-15a-a-2ab+4
=10ab-2ab-15a-a+4
=8ab-16a+4

(10)　　20/(21x^2 ) y^2×15x/44y÷25/77 xy-13/(14x^2 )
=(20y^2)/(21x^2 )×15x/44y×77/25xy-13/(14x^2 )
=(5×4y^2×3×5x×7×11)/(3×7x^2×4×11y×5^2 xy)-13/(14x^2 )
=1/x^2 -13/(14x^2 )=14/(14x^2 )-13/(14x^2 )=1/(14x^2 )

式の計算　基本問題

問題1

(1)(2)は値を求め、(3)(4)は方程式を解け

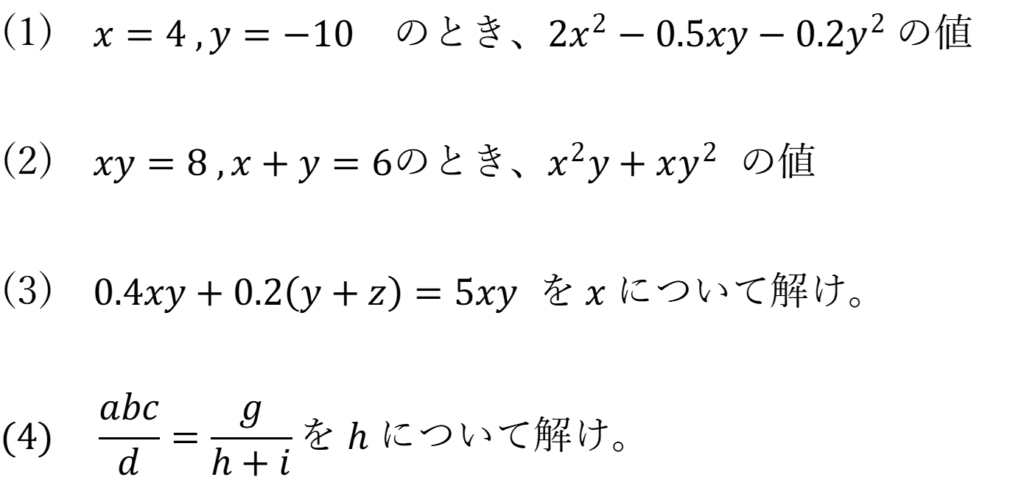
(1)　x=4 ,y=-10　のとき、2x^2-0.5xy-0.2y^2 の値

(2)　xy=8 ,x+y=6のとき、x^2 y+xy^2 の値

(3)　0.4xy+0.2(y+z)=5xy を x について解け。

(4)　abc/d=g/(h+i) をhについて解け。

解答を見る

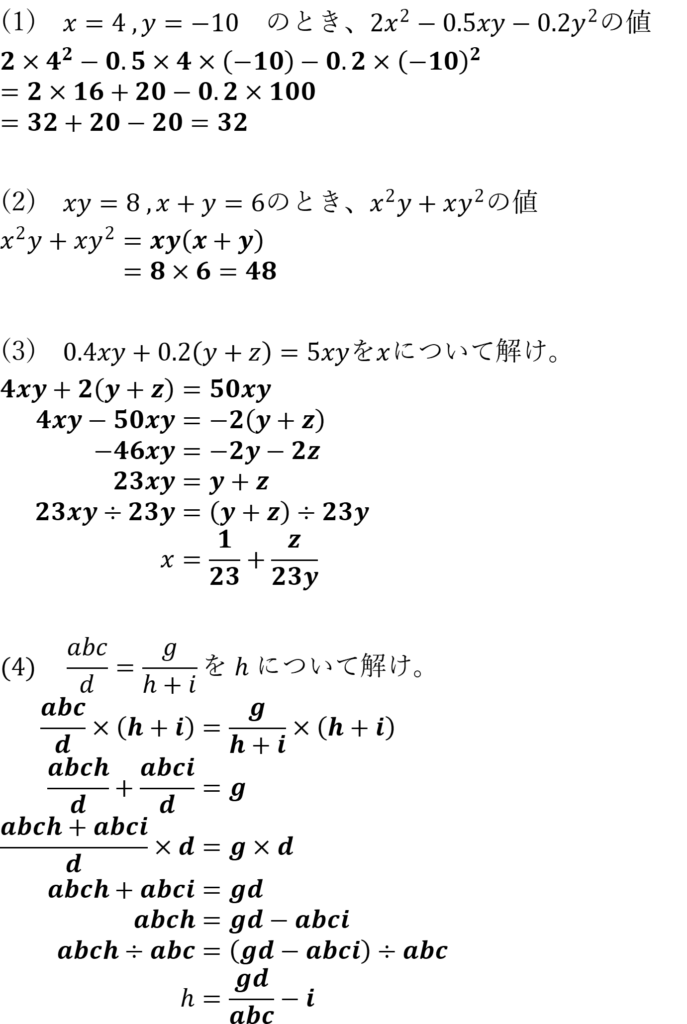
(1)　x=4 ,y=-10　のとき、2x^2-0.5xy-0.2y^2の値
2×4^2-0.5×4×(-10)-0.2×(-10)^2
=2×16+20-0.2×100
=32+20-20=32

(2)　xy=8 ,x+y=6のとき、x^2 y+xy^2の値
x^2 y+xy^2=xy(x+y)
=8×6=48

(3)　0.4xy+0.2(y+z)=5xyをxについて解け。
4xy+2(y+z)=50xy
4xy-50xy=-2(y+z)
-46xy=-2y-2z
23xy=y+z
23xy÷23y=(y+z)÷23y
x=1/23+z/23y

(4)　abc/d=g/(h+i) をhについて解け。
abc/d×(h+i)=g/(h+i)×(h+i)
abch/d+abci/d=g
(abch+abci)/d×d=g×d
abch+abci=gd
abch=gd-abci
abch÷abc=(gd-abci)÷abc
h=gd/abc-i

問題2

連続する3つの奇数の和が3の倍数になることを説明しなさい。

解答を見る

連続する3つの奇数を、整数nを用いて、
2n+1 ,2n+3 ,2n+5 とすると、3つの奇数の和は
(2n+1)+(2n+3)+(2n+5)
=2n+2n+2n+1+3+5=6n+9=3(2n+3)
nは整数より、2n+3も整数であるから、
3(2n+3)は3の倍数である。
したがって、連続する3つの奇数の和は3の倍数になる。

問題3

半径4Rの球の表面積は、半径2Rの円の面積の何倍か、求めなさい。

解答を見る

半径4Rの球の表面積は4πr^2より、4π×(4R)^2=64πR^2
半径2Rの円の面積は、πr^2より、π×(2R)^2=4πR^2
64πR^2÷4πR^2=16　したがって16倍

よかったらシェアしてね！

URLをコピーしました！