対応科目数学の画像
小学生、中学生の対応科目算数、数学の欄には、数式の画像を添付しています。
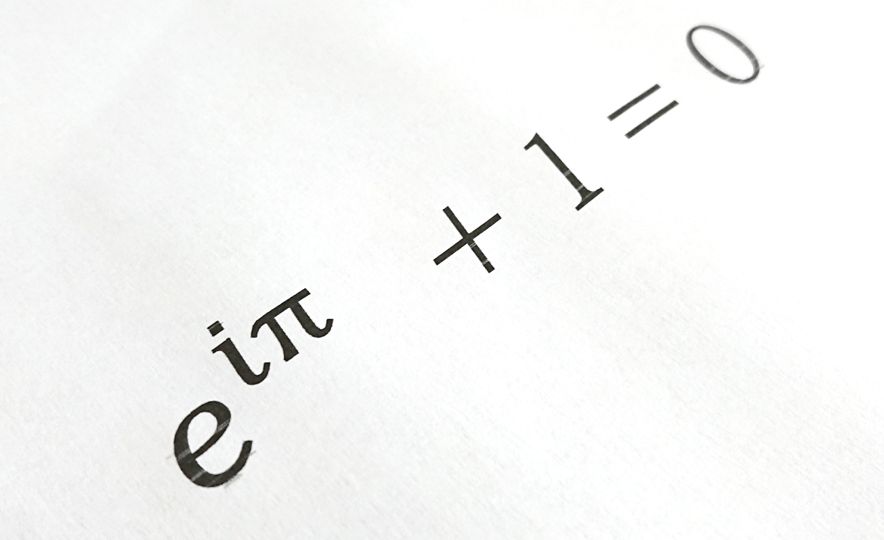
こちらの式は、小学校、中学校で習うものではありません。
いったいどういう意味なのか、紹介していきます。
オイラーの等式
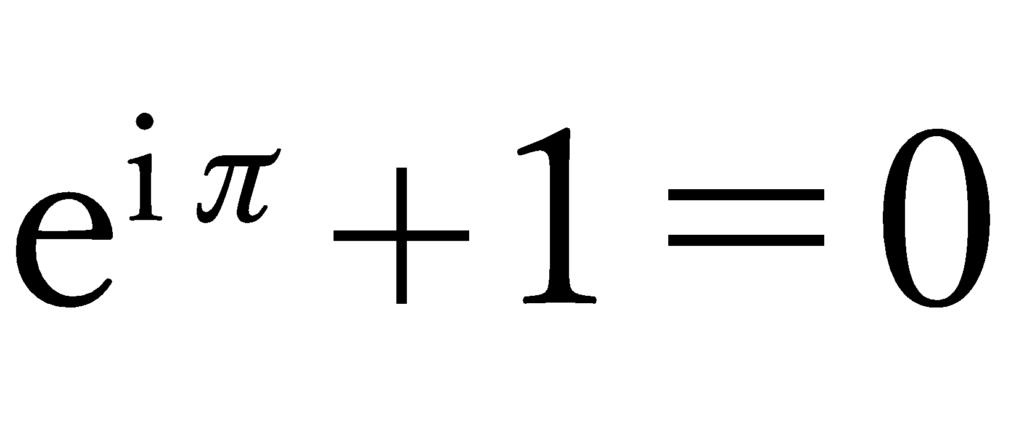
この式はオイラーの等式という名前です。
世界で最も美しい数式と言われています。
小学生、中学生にとっては何がなんだかわからないと思うので、なるべくわかるように説明していきたいと思います。
使われている記号について①
まず、使われている記号がいったい何なのかということから説明していきます。
数字の1と0、+、=はわかると思います。問題はeとiとπですね。
最もわかりやすいπから説明していきます。
中学生になると学習するのですが、πとは円周率のことです。
小学生でも高学年になると円周率を習います。円周率というのは、円の面積や、円のまわりの長さを求めるときに必要になってくる数字のことです。
円は常に一定の形をしているので、直径(あるいは半径)が変わるだけで、円の面積も円のまわりの長さも決まってしまいます。
直径1cmの円の周りの長さが何cmなのか、とことん調べた結果、3.1415926535897932384626433832…cmと無限に続いてしまうような数になってしまいました。これを円周率と言います。
1÷3=0.33333…のように同じ数の繰り返しではなく、全くことなる順番で数字が来てしまい、決まった法則も見つけることができませんでした。0.33333…は分数で1/3と表すことができますが、この3.14159265358979…は分数で表すこともできません。
このように、普通の数字で表すことができない、人間には理解できない数字を無理数と言います。この円周率も無理数の一つで、小学生の間は3.14で、中学生以降になるとπという記号を使って表すように決められています。
円周率=3.14…=πとして覚えておきましょう。
使われている記号について②
続いて、iを見ていきましょう。
iはいったい何を意味するのか、高校生になると学習します。ここでは簡単に説明していきます。
同じ数を2回かけることを2乗(じょう)すると言います。例えば、3×3は3の2乗と言います。

3の2乗と書くときはこのように書きます。数字の右上に小さく2と書きます。
同じように3回かける場合は3乗で、右上の小さい数字を3に、他の数字や記号の時も同じです。
3の2乗の答えは9とすぐにわかると思います。5の2乗は25、7の2乗は49というように、どのような数でもわかるのではないでしょうか。
では、2乗して4になる数字はいくつでしょうか。答えは2です。2×2=4となりますので、反対の操作も簡単ですね。
同じように、2乗して16になる数字は4、2乗して81になる数字は9ということになります。
では、2乗して1になる数字はいくつでしょうか。
答えは1ですね。
これは簡単です。それでは、2乗して-1になる数字はいくつでしょうか。
小学生はわからないと思うので、-1はマイナス1と言います。マイナスは0よりの下の数字のことを表します。気温でマイナス5℃とか聞いたことがあると思います。
2回かけてマイナスになる数は中学生ならあり得ないと答えるのが正解です。(-2)×(-2)=4のように、マイナスを2回かけると答えはプラスになりますから、マイナス同士をかけてもいけません。同じ数字を二回かけるので、マイナスを片方にだけかけることもダメです。
2回同じ数をかけて-1になる数字は、数字では表すことができません。しかし、数学の世界ではこの数を使わないと説明できないことが出てきます。そこで、2回かけて-1となる数をiと表すことにしました。読み方はアイです。
このiのことを本来はあり得ない数字のため、虚数と言います。少し難しかったと思いますが、簡単にまとめます。
2回かけて-1になる数字のことをiと表します。
i×i=-1というのが、最もシンプルな説明です。
使われている記号について③
最後に、eについて説明します。
eはネイピア数と言います。
ネイピア数を本格的に説明すると、複雑な内容になってしまうため、ここでは大雑把に紹介します。
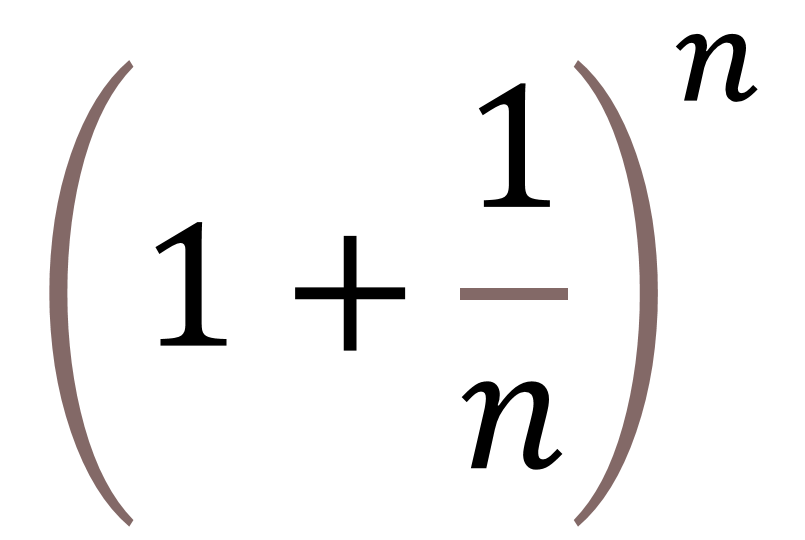
上の式で、nに数字を当てはめていきます。右上の小さいnは先ほど説明した通り、n回かけるという意味です。
例えば、nに1を当てはめると、(1+1)=2となります。
nに2を当てはめると、(1+1/2)×(1+1/2)=2.25
nに3を当てはめると、(1+1/3)×(1+1/3)×(1+1/3)=2.37037
nに4を当てはめると、(1+1/4)×(1+1/4)×(1+1/4)×(1+1/4)=2.441406
nに5を当てはめると、(1+1/5)×(1+1/5)×(1+1/5)×(1+1/5)×(1+1/5)=2.48832となります。
このnをだんだん大きくしていくと、限りなく大きくなってしまうように思えるかもしれませんが、ある一定の数に近づいていきます。
このnを無限に近づけていった場合、2.71828182845904523536…と無限に続く数となってしまいます。この数のことをeと表すことにしました。
そのため、このeもπと同じように、理解することができない無理数という位置づけになります。
数式の意味
ここで、はじめのオイラーの等式に戻りましょう。
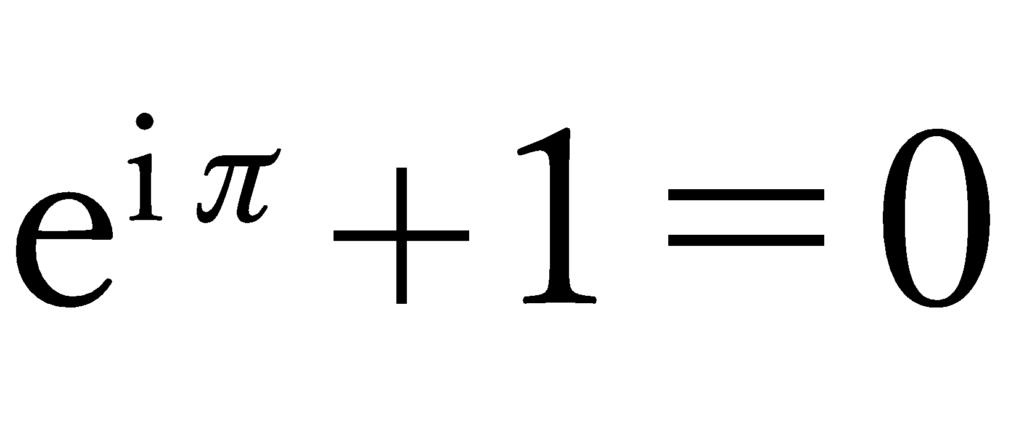
eもiもπも無理数や虚数で、普通に使う数とは大きく違った性質をしていることが分かったと思います。
それぞれが意味するものも、全く違っていて、関連は無いように思えます。
しかし、このオイラーの等式はこの異質な数をうまく組み合わせることで、非常にわかりやすい式に表すことができています。
e(ネイピア数)をi(虚数)×π(円周率)回かけたものに、1を足すと0になるという驚きの式です。
このような式あり得ないと思うかもしれませんが、しっかりと成り立ちます。
小学生や中学生では意味が分からないと思います。これがわかるようになるのが、高等数学です。
数学の大切さ
この理解ができないようなe、i、πの組み合わせに1という整数を足すと0という何もない状態になる。
これがオイラーの等式が最も美しい数式といわれる理由です。
このように、思いもしないような事柄を理解しようとして、様々な人たちが知恵を振り絞って導き出してきたのが数学の世界です。
小学校や中学校、高校で習った数学なんて、こんな内容将来使わないだろうと思うようなものがたくさんあると思います。複雑な数学は使わなくても生きていくことはできます。
しかし、この複雑な数学の世界がなければ、今の世の中は成り立っていません。数学が無ければスマホもゲームもインターネットもありませんし、ものの大きさもバラバラで、一日が何時間なのかという考えもそもそもありません。誰が何歳で、どこまで何mでということもわかりません。
人間は考える葦(あし)です。数学を考えられない人間は動物と同じです。
ただ言われたことをやり、自分で考えようとしない人間は動物と何が違うでしょうか。
これからの社会は人工知能がどんどんたくさんの職を奪っていく時代です。欲のままに生きているだけで動物と同じように自分で考えない人間が、まともに生きていくことができるでしょうか。
これからの社会で普通に生活していくためには、しっかり自分で考える力が必要になります。
その考える力を最も効果的に鍛えることができるのが、数学の世界です。数学が他の教科と大きく異なっている点はここにあります。
物事を論理的に考え、整理し、答えを導き出す一連の流れを通して、考える力を身に着けていく学問が数学だと私は思います。もちろん、理解した数学は全く使わないものばかりではなく、多くの人にとってほとんどが実社会で役に立つものばかりです。
さらに、この考える力は理性とも捉えることができます。
未来のことを考えず、今の欲望のままに生きていては動物と同じです。自分の欲を理性でもって抑えるためには、考える力が欠かせません。未来のことをどれだけ考えられるかで、目の前の欲望との向き合い方も変わってくると思います。
この考える力を小学生、中学生のうちからしっかり鍛えておく必要があるということはわかったと思います。
他の科目にはない考える力を鍛えるためにも、数学が必要です。
今のうちから数学はしっかりと勉強しておきましょう。
また、普段の生活でも自分で考えるということを大切にしてもらいたいと思います。
最後までお読みいただきありがとうございました。
